Ws for Open Systems on a PV Diagram
SISO, Internally Reversible, SS
Negligible changes in kinetic and potential energies
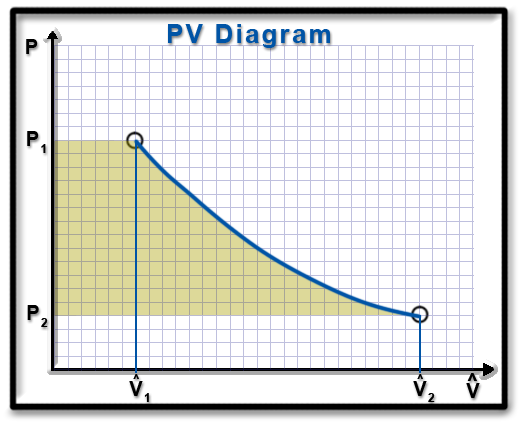
Polytropic
processes:Or:
Therefore:
Confused and have questions? We've got answers. With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field. If you rather get 1:1 study help, try 30 minutes of free online tutoring with Chegg Tutors.
© B-Cubed, 2003, 2005, 2006, 2014, 2018. All rights reserved.
Roll your mouse over this box to close.
Join Learn Thermodynamics Advantage
- Download Data Tables
- Download Study Aids
- Homework problem hints and answers
- Get Help from Dr. B in the LT Blog
- 120 day membership
Get it ALL for $5 US
